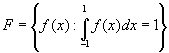
5.2 Determine the given subset of C[-1,1] is also a vector space.
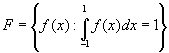
5.3 Express the given vector v as a linear combination of vectors in the set Q
![]()
![]()
5.4 Is the set Q above a basis for P2? Explain.
Given the set 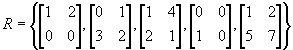
Find a subset of R that also spans the same space as R.
5.5 What is the dimension of the span of R above?
What is the dimension of the vector space of all 2x2 matrices?
Explain why R is not a basis for the space of all 2x2 matrices.
5.7 Suppose T:P2 to P4 is a linear transformation where T(1)=x4, T(x+1)=x2, T(3 + x + x2)=1 + x
Find T(2 + x + x2 )
5.8 Find T-1(x4 + x + 1)