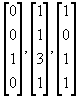
MCCC MAT203 Linear Algebra Prof. Porter's SAMPLE EXAM 2

  1. Use Gram-Schmidt process to generate an orthogonal set from the linearly independent vectors.

    2. Normalize any two of the vectors above.

    What would the set be called if all the vectors are normal?

  2. Given the Function,

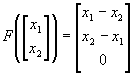
    3. Evaluate:

    Determine if the function is a linear transformation.

    For the given linear transformation, find the matrix A.

    Describe the null space and range.

  3. Find the least-squares quadratic fit to the given data. Show the work, plot points and graph.
    4.

    X

    1

    2

    3

    4

    Y

    3

    2

    3

    5

     

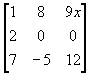
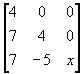
  4. Find the determinant of the matrix

  5. Given the matrix:

    6. Show how you would find the eigenvalues.

    Give the characteristic polynomial.

    Give the eigenvalues.

    What is the algebraic multiplicity?

    If x=2 Find the eigenvectors.

    Is the matrix defective? Why?

  6. Given the matrix:

    7. Give the eigenvalues.

    Give the eigenvectors

  7. Given:

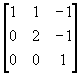
Determine if the matrix is diagonalizable.

If so, diagonalize it.

Calculate