Prof. Porter’s    MAT251 Multivariable Calculus   Sample- Third Exam

 

1.     Really take some time and tell me HOW multivariable calculus can be used in your field of study.

 

2.     You are asked to design a building that is over 15 stories tall with a square base and a sloping flat top with one corner the highest and one corner the lowest. Assume that each story is at least 10 feet. Identify the coordinates of at least three roof corner points, give the equation of the function for the roof, and then give the double integral that could be used to calculate the volume of the building.

 

3.     Show the triple integral that could be used to find the volume of the building from the last full story to the top of the highest corner.

 

4.     Because of gravity, the density of the building is higher at the base than the top. The density function is given by the formula δ(x,y,z)=100/(z+10) pounds per cubic foot. Give the integral that can be used to find total mass of your building.

 

5.     Give the integral that can be used to evaluate how high is the center of gravity? A building is considered unstable if its center of gravity is higher than the  length of the shortest side. Is your building unstable?

 

6.     To cut corners (literally), you are asked to make the design of the building perfectly round at the base. Using the same roof design, what would the integral that yielded the new volume of the building look like?

 

7.     You wonder if the volume of the cylindrical building would be easier to find in different coordinates. Give the integral for the volume if it was changed to cylindrical coordinates. Do not solve, but is it easier?

 

8.     Whenever you change from one coordinate system to the other for calculating the volume, there may be changes in  the dV part. Set up the determinant that can be used to show that dv becomes when changing from rectangular to spherical coordinates.

 

9.     You decide to accent you building with a pure gold cover to the roof. Give the integral that would tell how much surface area has to be covered with gold.

 

10.                        Extend the ideas of triple integration to reduce this quintuple integral into a triple.

    

 

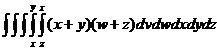
11.                         Give and graph a conservative vector field.

                   Find divF and curlF

                   Give

 

                                      Or

 

          Find  if F(x,y,z) = <4x,2,2y> and G(x,y,z) = 2xi – yj +zk

 

12.                         Find the integral under f(x,y) = x+2y and over the curve y=x(x+1) when x is between 1 and 2

 

                                  Or

 

     If C is defined by x = 2cost and y = 4sint for 0<t<π/4

 

     Find

 

13.                         How much work is done when you move in a strait line from (0,0) to (1,2) through the conservative vector field given by the potential function is xy?

 

                                  Or

 

     Find the exact value of using any method if

     F(x,y) = <2xy,x2+cosy> and C: r(t) = <t,tcos(t/3)> for 0<t<π

 

14.                        How much work is done in problem #13 if you follow the path that forms a unit square centered around the origin? Justify your answer.

 

                                  Or

 

     If C is the unit circle centered at the origning and F(x,y) = <x,y> then

     Find the exact value of

 

15.                        Give a non-trivial example of Greens theorem and solve it.

 

                                      Or

     Find if C are two cirles of radius 1 and 2 centered at the origin.