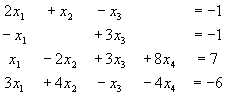
Linear Algebra MAT203

SAMPLE TEST 1

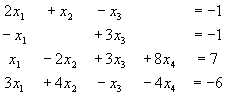
  1. Give the coefficient matrix for the system:

    2. Suppose that x3 is found to be zero. Give a simpler augmented matrix that could be used to solve the system.

  2. Use row operations to put the system above in row echelon form.

    3. Then put the system in reduced row echelon form.

    What is the solution?

  3. Find the equation of the parabola going thru the points (-2,120,(0,6),(2,4)
  4. Find (A+B)C if given the following:

  5. Find BTB. Is it symmetric? Find ||AC - BC||
  6. Are the following vectors linearly independant?

  7. For question number 1( part 2 where x3 is known), how would you solve for the inverse without a calculator?

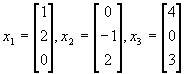
    8. Calculate the inverse and use it to solve the system.

  8. Give a geometric interpretation for :

  9. Determine if the above subset is subspace. Show all work.

    10.  

     

  10. Find the null space for the Matrix:

  11. Find the range for the matrix above.

    12.  

  12. Find a matrix B so that the span of the column space of A is equivalent to the column space of B.
  13. Find a subset of S that spans S

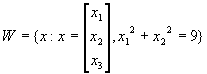
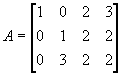
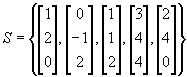
    14. Show the method you use.

  14. Find a basis for the null space of the matrix A whose column vectors are S above.
  15. Give the nullity and the rank for the matrix.

Can you find a basis for the range of A in 14?