Content Material

By Michael Dorneman
Associate Professor of Chemistry
Mercer County Community College
Trenton, NJ

• Student Directions: Printable Word Document

• Overview

  There are over 8,000 artificial objects in orbit around the Earth, many of which are operational satellites. Satellites fulfill a wide variety of missions, including recording weather, environmental, and espionage data about the Earth, relaying communications (cell phones, TV, radio), locating people and places (Global Positioning Satellites), and looking out into the Universe, among others.

  For the satellite to stay in a circular orbit around the Earth instead of shooting out into space, it must have centripetal force acting on it. One can calculate the centripetal force on the satellite using Newton’s Second Law:

           F  =  m a

To do this one must use the mass of the satellite and the acceleration due to the centripetal force:

Where v is the velocity of the satellite. The “r” is the radius of the circular orbit.

For your satellite “r” is the distance to the center of the Earth. So “r” must be calculated by adding the radius of the earth and the altitude of the satellite.

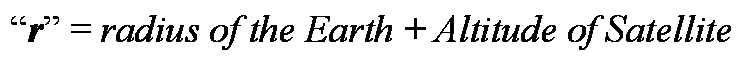
Now, remember that the force keeping the satellite in circular motion (in orbit) around the Earth, the centripetal force, is (equals) the Force of Gravity. Newton’s Law of Universal Gravitation relates the Force of Gravity on an object to the mass of the object, the distance between the object and the center of the Earth, and the mass of the Earth. Newton’s Law of Universal Gravitation is:

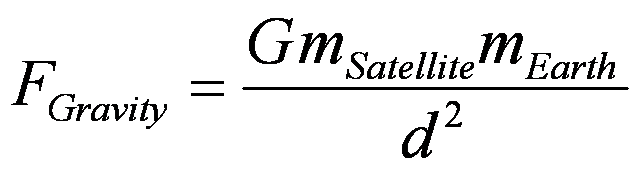
With these formulas, and a bit of algebra, one can calculate the mass of the Earth.

So, in summary:

1. From the altitude of the satellite and the radius of the Earth, you can calculate the radius of the orbit of the satellite, “r”
2. From the radius of the orbit of the satellite, “r”, and the velocity of the satellite, v, you can calculate the centripetal acceleration, acentripetal
3. From the centripetal acceleration, acentripetal and the mass of the satellite you can calculate the centripetal force, Fcentripetal, with Newton’s Second Law.
4. The centripetal force, Fcentripetal , is (equals) the Force of Gravity on the satellite, From the Force of Gravity on the satellite, the mass of the satellite, and the distance between the satellite and the center of the Earth “r”, you can calculate the mass of the Earth.

Procedure:

Data Collection:
You will need to record all data and numbers that you use on the worksheet, and clearly demonstrate the calculations in the format you have used in lab, also on the worksheet. Fill in the worksheet as you do this exercise. If you have a Pop-up blocker, you may want to set it to allow Pop-ups from NASA.

Go to http://science.nasa.gov/RealTime/ and read about J-Track 3D. About how many artificial objects are in orbit around the Earth? How many of these are satellites? On the menu on the left side of the screen, click on J-TRACK 3D (if asked, run the application from NASA).

After the small window fully loads and displays, each white dot in the picture will represent the real time location of a satellite. Clicking on a dot reveals that satellites designation or name, and the circle or oval that represents its orbit. Click on a few satellites. Find one that is close to the Earth, with a circular orbit, but DO NOT use an Iridium satellite (their masses are not recorded). Now, find the menu in the upper left hand corner of the J-Track 3D window, and pick View and then Satellite Position. Record the designation or name of the satellite, its altitude, and velocity. Be certain to include the units for those measurements.

Now go to the NSSDC Master Catalog Spacecraft Query Form: http://nssdc.gsfc.nasa.gov/nmc/sc-query.html  You must use a satellite for which the On-orbit dry mass is given. Type the name of your satellite into the Query Form. Do not include the number. (There may be no data for a specific satellite, but there will be data for many other members in the group.) Click on the Submit button. It may take a few minutes to search the NSSDC Master Catalog. Read about your satellite, find and record its mass (called On-orbit dry mass). If information for your satellite is not available, or you get an error message, go back to the J-Track 3D window and pick a different satellite. You may have to try several satellites.

You cannot do the exercise without the Name (and number), Mass (On-orbit dry mass), Velocity, and Altitude of a satellite in orbit around the Earth.

You will need two other pieces of data, the radius of the Earth and a value for G, the Gravitational Constant. The radius of the Earth is located at Earth Facts:
http://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html
Based on the direction of the orbit of your satellite, record and label the more appropriate radius of the Earth. For the Gravitational constant G we will use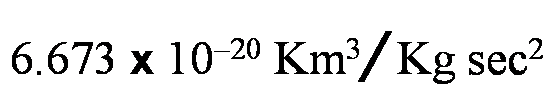

Calculations:

1. Calculate “r” for your satellite:
              “r” = radius of the Earth + Altitude of Satellite
     Units on your answer will be in kilometers. This is the value for d used in step 4

2. Calculate the centripetal acceleration, acentripetal . When you square vsatellite use parentheses to include the units.

 

    Units on your answer will be in kilometers/second squared.

3. Calculate F centripetal, with Newton’s Second Law:

    Units on your answer will be in kilonewtons (KN). 1 KN = 224.8 lbs.

4. Calculate the mass of the Earth mEarth from Newton’s Law of Universal Gravitation,
     after rearrangement for m Earth:
 

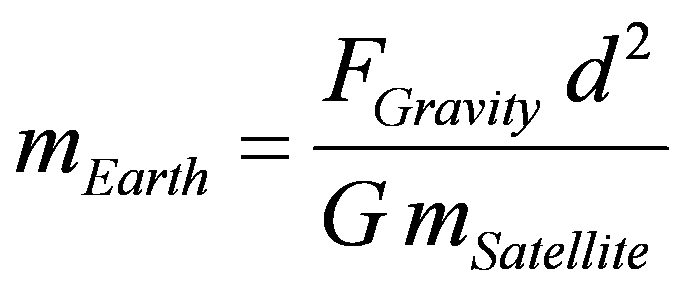
Remember, d is the distance between the center of the Earth and the satellite, calculated earlier. Units on your answer will be in kilograms.

Answer the following questions on the worksheet:

• What is the mass of the satellite?
• What is another name for the force of gravity on an object?
• What is the weight of the satellite (from the perspective of the Earth)?
• From the perspective of the satellite, what is the weight of the Earth? Why? (Hint, Newton’s Third Law of Motion)
• What is the difference between Mass and Weight?

---

Worksheet: Printable Word Document

Name:__________________________ Class________ Ref. Num. _______

Data:

Satellite Designation:  ___________________________________________

Satellite Mass m Satellite =                    Satellite Velocity, vSatellite =

Satellite Altitude =                             Radius of the Earth =

Gravitational Constant, G =

Calculations:

For each step, write the formula first, then replace the variables with measurements (include units) then calculate and write your answer.

Calculation of “r” for your satellite:    (Note, this is also d for the Mass of the Earth calculation.)

 

 

 

 

 

 

 

 

Calculation of the centripetal acceleration, a centripetal

 

 

 

 

 

 

 

 

 

 

 

 

 

Calculation of the centripetal force, F centripetal:

 

 

 

 

 

 

 

Calculation of the Mass of the Earth:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

What is the accepted value
of the Mass of the Earth?      _____________________________________

Try to explain why your calculated value for the Mass of the Earth is different from the accepted value. Note, calculation error is not acceptable as an explanation.

 

 

What is the mass of the satellite? ____________________________________

What is another name for the
force of gravity on an object?    _____________________________________

What is the weight of the satellite
(from the perspective of the Earth)? _________________________________

From the perspective of the satellite,
what is the weight of the Earth? _____________________________________

Why? (Hint, one of Newton’s Laws of Motion)

 

What is the difference between Mass and Weight?